算法:双指针

一、移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例1：

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

示例 2:

输入: nums = [0]
输出: [0]

题解：

定义两个指针， left 和 right 。 left 从索引 0 开始， right 也从索引 0 开始。
遍历数组，使用 right 指针。
当 right 指针指向的元素不是零时：
- 将 left 指针指向的元素（如果它是一个零）替换为 right 指针指向的元素。
- 将 left 指针向前移动一位。
当 right 指针指向的元素是零时，继续向右移动 right 指针，直到找到一个非零元素或到达数组末尾。
重复步骤 3 和 4，直到 right 指针到达数组末尾。
当 right 指针遍历完成后， left 指针之前的所有元素都是非零的，并且保持了原始顺序。此时，将 left 指针之后的所有位置填充为零。

var moveZeroes = function(nums) {
    let left = 0; // 初始化左指针
    for (let right = 0; right < nums.length; right++) {
        if (nums[right] !== 0) {
            // 交换 left 指针和 right 指针指向的元素
            nums[left] = nums[right];
            // 只有当交换了元素后，left 指针才向前移动
            left++;
        }
    }
    // 用零填充 left 指针之后的所有位置
    while (left < nums.length) {
        nums[left] = 0;
        left++;
    }
    return nums;
};

二、盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i])

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例1：

输入：[1,8,6,2,5,4,8,3,7]
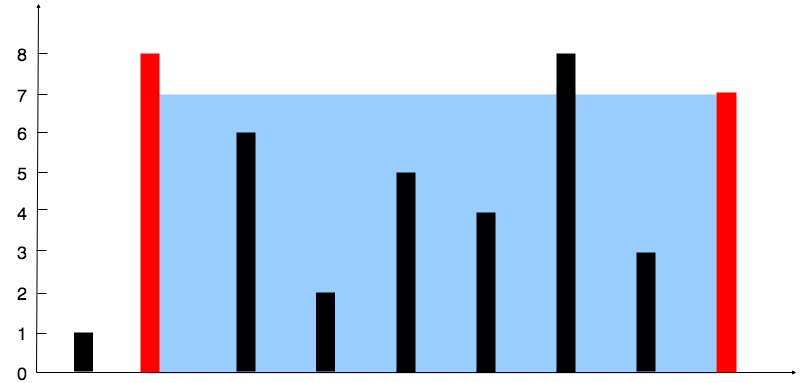
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例2：

输入：height = [1,1]
输出：1

题解：

初始化两个指针 l 和 r ，分别指向数组 height 的起始和结束位置，即 l = 0 和 r = n - 1 。
定义一个变量 maxWater 来存储最大水量，初始值为 0。
当 l < r 时，执行以下操作：
- 计算当前左右指针高度的较小值，记为 minHeight 。
- 计算当前容器的容量，即 minHeight 和指针之间的距离（ r - l ）的乘积，记为 currentWater 。
- 如果 currentWater 大于 maxWater ，则更新 maxWater 。
- 如果左边的高度小于右边的高度，移动左指针 l 向右一位（ l++ ），否则移动右指针 r 向左一位（ r– ）。
当 l 和 r 相遇或交叉时，结束循环。
返回 maxWater 。

var maxArea = function(height) {
    let l = 0, r = height.length - 1;
    let maxWater = 0;
    while (l < r) {
        let minHeight = Math.min(height[l], height[r]);
        let currentWater = minHeight * (r - l);
        maxWater = Math.max(maxWater, currentWater);
        if (height[l] < height[r]) {
            l++;
        } else {
            r--;
        }
    }
    return maxWater;
};

三、三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

题解：

排序：首先对数组 nums 进行排序。
初始化：设置三个指针 i 、 left 和 right 。 i 从索引 0 开始遍历数组， left 和 right 分别指向 i 之后的两个端点。
遍历：对于每个 i ：
- 设置 left 为 i + 1 ， right 为数组的最后一个索引。
- 执行循环，当 left < right 时：
- 计算当前三元组的和： sum = nums[i] + nums[left] + nums[right] 。
- 如果 sum 等于 0，找到了一个满足条件的三元组，将其添加到结果列表中，然后将 left 和 right 向中间移动，同时跳过重复的元素。
- 如果 sum 小于 0，说明需要增大和，因此将 left 向右移动（寻找更大的数）。
- 如果 sum 大于 0，说明需要减小和，因此将 right 向左移动（寻找更小的数）。

var threeSum = function(nums) {
    nums.sort((a, b) => a - b); // 对数组进行排序
    const result = [];
    for (let i = 0; i < nums.length - 2; i++) {
        if (i > 0 && nums[i] === nums[i - 1]) continue; // 跳过重复的元素
        let left = i + 1, right = nums.length - 1;
        while (left < right) {
            const sum = nums[i] + nums[left] + nums[right];
            if (sum === 0) {
                result.push([nums[i], nums[left], nums[right]]);
                left++;
                right--;
                // 跳过重复的元素
                while (left < right && nums[left] === nums[left - 1]) left++;
                while (left < right && nums[right] === nums[right + 1]) right--;
            } else if (sum < 0) {
                left++; // 需要增大和
            } else {
                right--; // 需要减小和
            }
        }
    }
    return result;
};

四、接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例2：

输入：height = [4,2,0,3,2,5]
输出：9

题解：

初始化：创建两个数组 leftMax 和 rightMax ，它们的长度与输入数组 height 相同。 leftMax[i] 表示索引 i 左侧最高的柱子高度， rightMax[i] 表示索引 i 右侧最高的柱子高度。
填充左侧最大高度数组：从左到右遍历 height 数组，对于每个索引 i ， leftMax[i] 初始化为 height[i] ，然后与 leftMax[i-1] 比较，取较大值。
填充右侧最大高度数组：从右到左遍历 height 数组，对于每个索引 i ， rightMax[i] 初始化为 height[i] ，然后与 rightMax[i+1] 比较，取较大值。
计算雨水量：遍历 height 数组，对于每个索引 i ，计算当前柱子能接的雨水量，即 min(leftMax[i], rightMax[i]) - height[i] 。如果这个值大于 0，累加到总雨水量 total 。
返回总雨水量。

var trap = function(height) {
    let n = height.length;
    let leftMax = new Array(n);
    let rightMax = new Array(n);
    let total = 0;

    // 初始化左侧最大高度数组
    leftMax[0] = height[0];
    for (let i = 1; i < n; i++) {
        leftMax[i] = Math.max(height[i], leftMax[i - 1]);
    }

    // 初始化右侧最大高度数组
    rightMax[n - 1] = height[n - 1];
    for (let i = n - 2; i >= 0; i--) {
        rightMax[i] = Math.max(height[i], rightMax[i + 1]);
    }

    // 计算雨水量
    for (let i = 0; i < n; i++) {
        total += Math.max(0, Math.min(leftMax[i], rightMax[i]) - height[i]);
    }

    return total;
};